چند نامساوی هندسی

تعریف: برای اعداد حقیقی نامنفی  ؛ میانگین هندسی را به صورت زیر تعریف می‌کنیم:

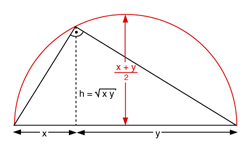
حکم: برای اعداد حقیقی نامنفی  ؛ میانگین هندسی از میانگین حسابی؛ نابیش‌تر است یعنی: .

پیش از پرداختن به اثبات این حکم، ابتدا لم زیر را می آوریم :
لم: اگر x عدد حقیقی نامنفی دلخواهی باشد آن‌گاه: .
این لم به کمک قضیه ی مقدار میانگین اثبات می شود و در کتب استاندارد حساب دیفرانسیل و انتگرال آمده است .

اثبات حکم: برای  ، با جایگذاری  در نامساوی لم خواهیم داشت:.و لذا:

۲- نامساوی اردوش- موردل:
حکم:اگر P نقطه‌ی دلخواهی درون مثلث  به ترتیب، فاصله‌ی P از اضلاع c,b,a باشند آن‌گاه:.
و تساوی برقرار است اگر و تنها اگر مثلّث ABC متساوی‌الاضلاع  بوده و P مرکز ثقل آن باشد.
اثبات:

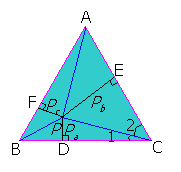
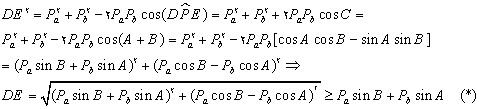
از طرفی چون چهارضلعی CDPE محاطی است پس طبق قضیه‌ی بطلمیوس داریم:

با استفاده از (**) داریم :

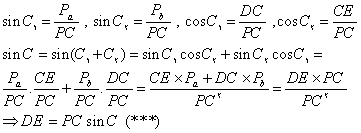
اکنون با استفاده از رابطه‌های (*) و (***) خواهیم داشت:.
به روش مشابه می‌توان نشان داد که:.
بنابراین:

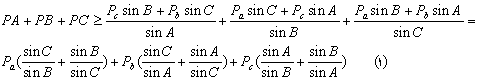
لم: برای ۰<x ،  و تساوی وقتی و فقط وقتی رخ می‌دهد که ۱=x.
اثبات لم به عنوان تمرین به خواننده واگذار می‌شود.
پس با استفاده از لم و رابطه‌ی (۱) خواهیم داشت:.

و تساوی وقتی و فقط وقتی رخ می‌دهد که مثلّث ABC متساوی‌الاضلاع بوده و P مرکز ثقل آن باشد.

نکته:نامساوی اردوش-موردل در حالتی که P روی مرز مثلّث ABC باشد نیز برقرار است.

۳- نامساوی اویلر:
حکم: اگر R شعاع دایره محیطی و r شعاع دایره محاطی مثلّث ABC باشند، آن‌گاه: .
لم: اگر d فاصله‌ی مرکز دایره‌ی محیطی و مرکز دایره‌ی محاطی مثلّث ABC باشد آن‌گاه:.

برای دیدن اثباتی از این لم می‌توانید به کتاب " بازآموزی و بازشناخت هندسه" ترجمه‌ی عبدالحسین مصحفی مراجعه نمائید.
به وضوح، حکم با توجه به لم فوق نتیجه می‌شود.

۴- نامساوی Hadwiger-Finsler:
حکم: اگر a,b,c اضلاع مثلّث ABC و A مساحت آن باشند، آن‌گاه:

پیش از پرداختن به اثبات حکم، مفهوم تابع محدّب را معرّفی می‌کنیم:
تعریف: تابع  را محدّب گوئیم (I یک بازه است) هرگاه به ازای هر x,y در I و هر  داشته باشیم:  .

لم: اگر f تابعی محدّب و  نقاط دلخواهی در دامنه‌ی f و اعداد دلخواه ,()طوری باشند که  آن‌گاه: 

اثبات لم با استقراء بر n .(جزئیات به عهده‌ی خواننده).
اثبات حکم:  که در آن  زاویه‌ی بین ضلع‌های b,cاست. چون  پس :

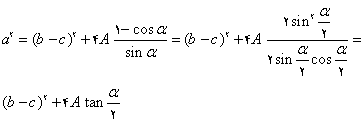
به روش مشابه می‌توان نشان داد که و که در آن  به ترتیب زوایای بین ضلع‌های "a,b" , "a,c "هستند. بنابراین:

چون  و  در  محدّب است. [چرا؟]
پس طبق لم اخیر خواهیم داشت:

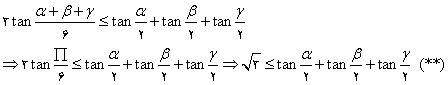
با استفاده از (*) و (**) خواهیم داشت:

و به این ترتیب حکم ثابت می‌شود.

۵- نامساوی Weizenbock:
حکم: اگر a,b,c اضلاع مثلّث ABC و A مساحت آن باشند، آن‌گاه:

اثبات: کافی است در نامساوی ۴ از این واقعیت که: است، استفاده کنیم.

منابع:

http://Planetmath.org
http://mathdb.org
http://mathworld.wolfram.com