مقاله را با طرح مساله ي زير آغاز مي كنيم:
مساله:مستطيل PQRS با طول و عرض به ترتيب 15 و 6 سانتيمتر را در نظر بگيريد.مساحت مثلث A برابر 4 سانتي متر مربع و مساحت مثلث B برابر 16سانتي متر مربع ميباشند. مساحت مستطيل C چقدر است؟
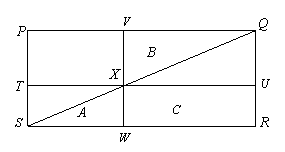
شكل 1
راه حل اول:مساحت مثلث SQR برابر است با: 45=2/(6×15).بنابراين مساحت مستطيل C چنين محاسبه خواهد شد: 25=4-16-45 .
راه حل دوم:با استفاده از قضيه ي تالس و با توجه به اين كه نسبت مساحت هاي دو مثلث B به A برابر 4 است پس:2=VQ/WS=VX/WX=QX/SX و لذا مساحت C برابر 20 سانتي متر مربع است.
در اين جا مي بينيد كه حل اين مساله به دو جواب مختلف منجر مي شود.اما مشكل كجاست؟
در حقيقت بايد گفت كه با فرض هاي مساله،X نمي تواند بر پاره خط SQ واقع شود.
اگر PT=a و VQ=b قرار دهيم آن گاه 16=2/(ab) و ![]() و لذا خواهيم داشت:
و لذا خواهيم داشت:![]() .از اين جا دو سري جواب به صورت زير به دست مي آوريم:
.از اين جا دو سري جواب به صورت زير به دست مي آوريم:
![]() و
و ![]()
![]() و
و ![]()
پس شكل مساله با توجه به مفروضات آن به يكي از دو صورت زير رسم مي شود:
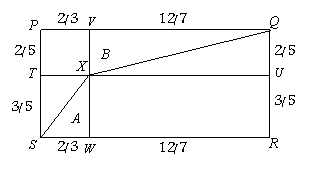
شكل 2
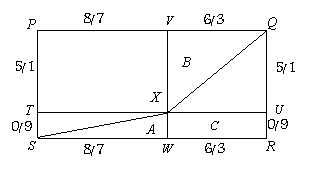
شكل 3
مساحت C در شكل 2 برابر ![]() و در شكل 3 برابر
و در شكل 3 برابر ![]() است .
است .
حالت ديگري كه مي توان در نظر گرفت از اين قرار است:(در اين حالت C ديگر مستطيل نيست.)

شكل 4
پارادوكس كيوري(Curry):
طرح مساله ي قبل ما را به سمت پارادوكس مشهوري به نام پارادوكس كيوري سوق مي دهد. در شكل زير در هر دو بخش چنين به نظر ميرسد كه يك مثلث قائم الزاويه به دو مثلث قائم الزاويه ي كوچكتر و يك مستطيل تقسيم شده است جز اين كه دومي يك واحد مربع كم تر دارد.در اولي مستطيل گوشه ي سمت راست پايين يك مستطيل 5×3 و در دومي يك مستطيل 8×2 ميباشد.
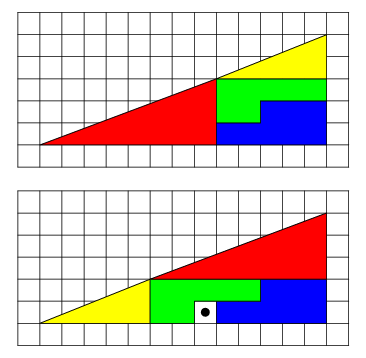
شكل 5
با مقايسهي شيب وترهاي سه مثلث قائم الزاويه در شكل 5 ميبينيم كه:
![]()
توضيحي كه در مورد اين پارادوكس مطرح ميشود اين است كه مثلث بزرگ در واقع يك مثلث نميباشد!وتر مثلث بزرگ شكستگي دارد كه در قسمت بالايي،اندكي متمايل به داخل است در حالي كه در قسمت پاييني،اندكي متمايل به خارج است.
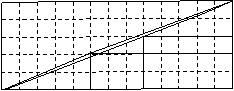
شكل 6
مساحت بين دو قطعه ي شكسته،برابر 1 واحد مربع است.
طول اضلاع مجاور به زاويه ي قائمه به طور تصادفي انتخاب نشدهاند.طول اين اضلاع در سه مثلث عبارت هستند از:(2 ، 5) ، (3 ، 8) و (5 ، 13) كه اعداد فيبوناتچي ميباشند.
حالت كلي پارادوكس:
اعداد فيبوناتچي به صورت زير تعريف ميشوند:
(![]() )
) ![]() و
و ![]()
اكنون در شكلي مانند شكل 5، اضلاع مجاور به زاويه ي قائمه ي مثلث ها را به صورت:![]() در نظر مي گيريم.
در نظر مي گيريم.
در اين لحظه،توجه شما را به اتحاد كاتالان جلب مي كنيم:
![]()
در اين رابطه،nوr اعداد طبيعي بوده و n>r است.(براي ديدن اثباتي از اين اتحاد به:www.planetmath.org مراجعه نماييد.)
با قرار دادن 2+n به جاي n و 2=r در اتحاد كاتالان داريم:
(*) ![]()
از طرفي:
(**) 
در روابط (*) و (**) براي n زوج ،هر دو عبارت مثبت خواهند بود و لذا خواهيم داشت: ![]() .
.
و همچنين براي n فرد،نتيجه ميشود كه :![]() .
.
اين كسرها در حقيقت،شيب سه وتر مثلث هاي قائم الزاويه هستند و همان توضيحي كه در حالت خاص آمد را براي حالت كلي پارادوكس،خواهيم داشت.
توضيح ديگري كه در مورد اين پارادوكس مي توان ارائه كرد بر اساس مقايسه ي مساحت ها است.در قسمت بالايي شكل 5 داريم:5/32=2/(5×13)=مساحت كه برابر است با:
32=5+12+15=مساحت مثلث زرد+مساحت مثلث قرمز+مساحت مستطيل
و اين تناقض است.
در قسمت پاييني شكل 5 نيز با يك روش،مساحت 32 واحد مربع و با روشي ديگر 5/31 واحد مربع مي شود كه تناقض است.
پارادوكس 65=64 :
اكنون بايد قادر باشيد كه مطلب زير را توجيه نماييد:

منبع:
www.math.nus.edu.sg


